The folding algorithm happens in a number of steps. Really we are looking to find a smooth transition between an initial layout an a final layout. In this example we show the list items A through N. Items A, B, and C are in the top fold. Items M and N are in the bottom fold. Items J and K are in the middle fold. Also, items E, H, and L are highlighted and must remain visible at all times.

When the user clicks on a fold, we need to take some action.

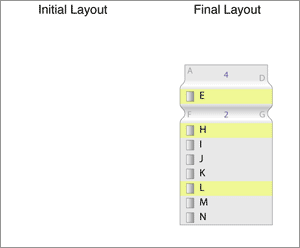
In this case, the user has clicked on the M-N tab. We need to transition to a new state where M and N are visible. That is, the "point of interest" is set to M. The algorithm is going to try to do a layout showing as many of the items around the "point of interest" as possible.
In the first attempt, we simply try to show the entire list.
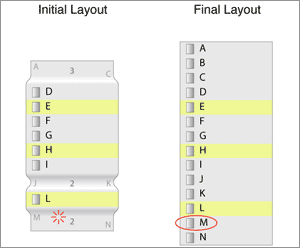
But, we also have to consider the size limits. We see that this layout is too large for the required size limits. Since our system has a circular system of constraints, we can't use a constraints based system to do the layout. Instead we do a binary search for the correct number of items to show around the "point of interest". We try a slightly smaller layout:
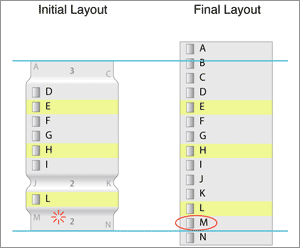
This layout fits within the required size range. However, we could do a little better, so we try to do a layout with more items than this, but less than our last approach (it's a binary search).
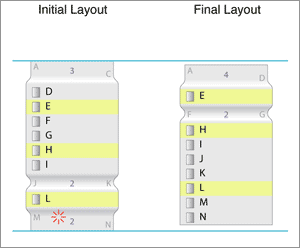
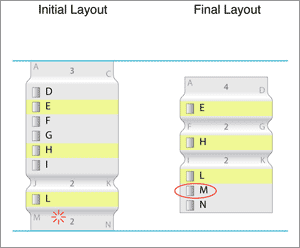
At this point, we have found the correct Final Layout that fits the size requirements as best as possible and shows the most items around the point of interest.
Now, we must start with the task of transitioning from one state to the next. In order to do this, we break apart the list in to a set of components. You will see that there are List components that show list items (like D,E,F, etc). There are also Fold components that show hidden items.
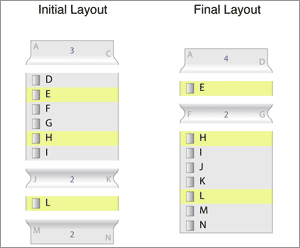
In order to transition smoothly from the initial layout to the final layout, we need decide which components will transition from their current state, into a state that visually represents part of the final layout. We also need to know which components will be created, or removed from the layouts, and where in the list they will grow-from or shrink-to during the animation of creation or removal.
In order to make room for components that are being created or destroyed, we do a segmentation step. First, we'll look for 1-to-2 matches from the initial layout to the final layout.
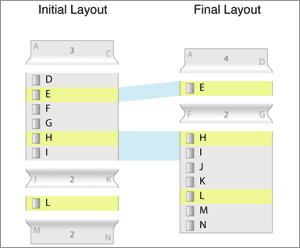
We see here that we count a connection when an overlap between components occur. In the image above, we have the D-I list in the initial layout overlaping with the E list and the H-N list in the final layout.
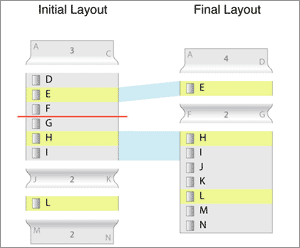
Since this is a 1-to-2 mapping, we segment the D-I list in order to break the 2-to-1 mapping.
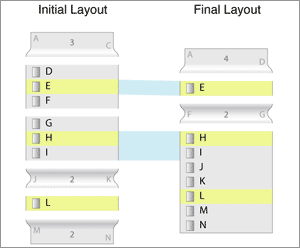
We break apart the component in the middle of the overlaps so that there are two 1-to-1 mappings. you can see now that the fold F-G in the final layout has a place to be inserted. It could not have transitioned from the J-K fold in the initial layout because it would have had to hop over the selected H list item.
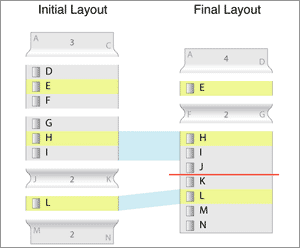
Next, we look for 2-to-1 mappings from the final layout to the initial layout.
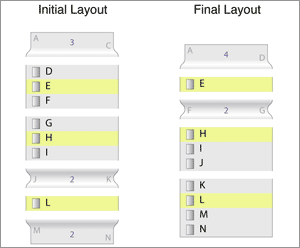
After we do the segmentation step, we have a number of components that are ready for transitioning. Some components will need to be created. We insert the fold F-G in the final layout. This fold will grow from a sliver to it's correct size. It needs to know the place to grow from, so we reference it to a gap between elements in the initial layout.
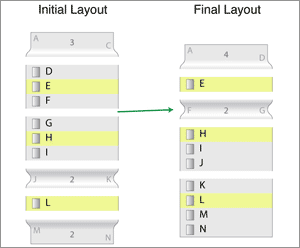
Similarly, Components must be removed during the transition. We find places for these components to disappear to:
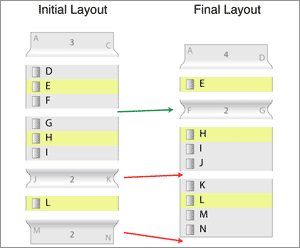
Every other component in this layout can smoothly transition from the initial layout to the final layout. Each component knows how to animate the transition to look fluid.
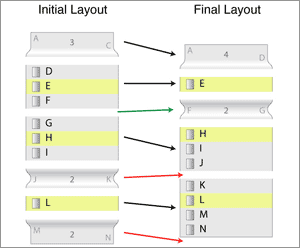
Finally, we run the visual transition trough the AnimationPlan module and the LookingGlass animation facilities. At this point, the folded scroll window smoothly transitions from the initial layout to the final layout.